Broken Symmetries 2

The idea of the series was engaging [Messiaen's] maximum attention during these years, and it was probably the influence of this fact that caused him to reflect on the possible strict, and strictly calculated, relationships on which his music might depend; there are many instances in these works of a clear conflict between spontaneity and organization, the one unwilling to abdicate and the other determined to become all powerful. This conflict, or antinomy, is reflected even in the titles of the different pieces written between 1949 and 1951 – Les Yeux dans les roues, Les Mains de l'abíme, Ile de feu.

– Pierre Boulez *

Olivier Messiaen

Île de feu II : no 4 de Quatre études de rythme : pour piano

Performed by Yvonne Loriod

( A score may be located through OCLC WorldCat )

Diagram 1
Compositional scheme of Île de feu 2
(Timings refer to the Loriod recording)

Descriptive Analysis (C2)

The previous post, Broken Symmetries 1, concentrated on the analytical dilemmas posed by the brief passage labelled C1 (mm. 70–75) in Diagram 1. C1 appears, as if out of nowhere, almost exactly half way through the piece as a stream of even pp legato 16th-note triplets. Architectonically, C1 only makes sense to me as a prefiguration of C2, the lengthy section I'm calling the 'Magma Dance' (this begins around 2:55 in the Loriod recording). Like C1, C2 is a double stream of 16th notes, one stream running in the right hand, the other in the left hand.

When I referred to C1 in the previous post as a passage of even triplets in two-voice 'first species counterpoint,' I wasn't entirely joking. Both C1 and C2 are instances of note-against-note counterpoint, but this is 'counterpoint-by-other-means.' I won't yet pursue, let alone formalize, the idea that is slowly emerging here and from other posts in this blog, but a better term for these passages – and many more in the contemporary literature – might be counterset. In our new, still tentative musical world, 'point' may refer to pitch, duration, dynamic, density, chord, key, silence, sample, noise, event, action, choice, instruction, function, feature, preference, intention – in short, any stuff that can make up a musical game of things-and-arrows from a mostly intuitive category theory.

But now to the story of Messiaen's notes and his (and my) 'conflict between spontaneity and organization.'

A C1 characteristic that I saved to discuss for comparison to C2 is the disjunct, narrow ranges occupied by each voice in C1. There the left hand spans the range C3–B3 while the right hand stays within the range C4–B4, disjunct from the left hand (Example 1a).[1]

Example 1a                                                   Example 1b

The C2 passage on the other hand was described by Messiaen as 'a cross-handed perpetual motion in the depths of the keyboard.'[2] Example 1b illustrates that the left hand's range in C2 is again bounded within a single octave. Down a fifth from the left hand in C1, it spans F2–E3. The ceiling of the right hand in C2 also drops a fifth from what it was in C1, taking the r.h. ceiling down from B4 to E4; but the r.h. floor drops from C4 down more than two octaves to Bb1, a fifth below the l.h. floor.  As we will soon see, all this 'down-a-fifth' into the depths of the keyboard activity associated with right- and left-hand ranges for the Magma Dance and its prefiguration will be accompanied by a related row transposition at the center of the big puzzle embedded in Île de feu 2.

A final contrasting element is that in C1 both hands are marked pp legato – but in C2 the right hand is marked f staccato against a 'ghosting' left hand that retains the C1 character as p legato. We'll now focus on the ghost in the left hand.

.      .      .      .

Diagram 2 is a numeric pitch-class transliteration of mm 92–131 so that the lines of the crossing hands can be clearly distinguished for analysis. Each strip represents two measures; the red lines indicate bar lines, the black vertical lines indicate Messiaen's 16th-note groupings. The top row of each strip transliterates the right hand & the bottom transliterates the left hand.

Diagram 2

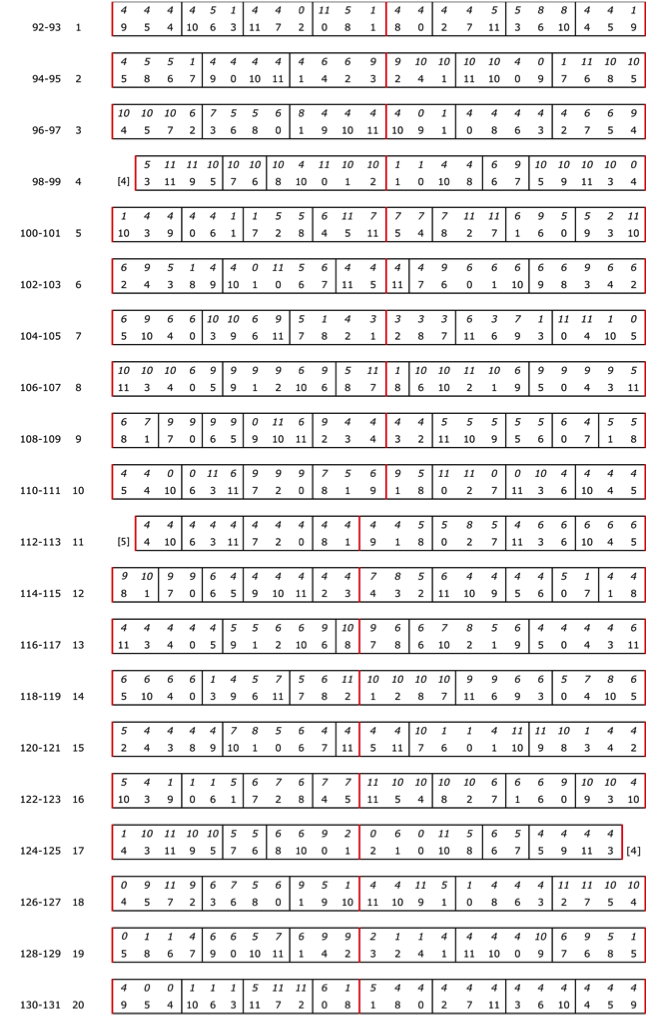
Let's consider the left hand (bottom half of the strips) which as noted previously spans only one octave, F2–E3. One is immediately struck by the fact that the l.h. in each pair of measures is a 23-note palindrome. So it is tempting to jump immediately to the conclusion that any given l.h. strip consists of a 'twelve-tone row' and its retrograde connected by a common tone as in, for example, the first strip (l.h. of mm. 92–93):

9–5–4–10–6–3–11–7–2–0–8–\  1  /–8–0–2–7–11–3–6–10–4–5–9

This symmetry has been pointed out elsewhere[3], but I have yet to find a source that notes a second symmetry hiding in the left hand, let alone a source that asks where these 'rows' came from and whether/how they are related to one another and to the right hand. One thing is certain. It is quite misleading to suggest that these pitch-class strings will turn out to be well behaved 'twelve-tone rows' because, as a first quick scan reveals, there isn't a single canonic serial transformation in sight beyond the distinct palindromes we just identified. If C2 were 'serial' in the usual sense that word is taught to be taken, it would mean C2 is a simple concatenation of ten distinct 'tone rows' (which would be somewhat of a record for just one minute of music, and a triumph of compositional randomization.

So we've arrived at Île de feu 2's big puzzle. Now let's see if we can solve it, or at least determine if it is solvable or not. We'll start by isolating the distinct pc-strings.

Diagram 3

Diagram 3 shows that there is a vertical reflective symmetry accompanying the horizontal reflective symmetry, turning C2's left hand part into a house of mirrors. Folding Diagram 3 right to left and then bottom to top yields a 10×12 matrix (Diagram 4).

Diagram 4

This simplifies the analytical focus since it means that, to discover any further relationships within C2 (beyond this two-fold mirror symmetry), we only need to look at any one of the quadrants, since any relationship between 'rows' (or columns, for that matter) in one quadrant will be duplicated or mirrored in the other three. Diagram 4 shows the upper left quadrant.[4] Any relationship we can find among these ten 12-tone strings will be duplicated in the other quadrants.

Antinomous Analysis (C2)

The ten interversions in sections B1, B2 and B3 (compositional scheme, Diagram 1) have been the focus of most commentary about this work. The passage C2 (mm. 92-131, distilled into the matrix shown in Diagram 4), although it is one forth of the entire piece, has been ignored. But the C2 passage is Île de feu's maddeningly elusive big puzzle. Where do these ten strings come from and how are they related to one another (and/or possibly to material outside C2)? The story here is not, as in the fictive analysis of C1 in the previous post, centered on a single anomaly for which we can make up a likely scenario. The analysis below will be seen (at least for now) to describe either an unsolved solvable puzzle or one that has no solution. Such a description is what I mean by 'antinomous analysis.'[5]

All that our strictly descriptive analysis of C2 has given us so far are compelling clues scattered about, any one of which might be ignored as anomalous, but which taken together strongly suggest an as yet undiscovered over-arching pattern which we are compelled to pursue, not knowing whether or not we are running down a blind alley.

So let's begin by trying to find in Diagram 4 all the indisputably non-random features as well as noting the features that suggest randomness.[6] Following is a list of seven compositional features in C2. Each feature is followed by an analytical judgement:
   [✓] = functionally determined,
   [?] = 'non liquet' ('it is not clear'), i.e., suggestive of a functional relationship that remains undiscovered, or
   [✕] = tentatively random (no obvious evidence for either [✓] or [?]).

(1.) To reiterate from the descriptive analysis above, the entire passage in the left hand has a two-fold mirror symmetry. And if you connect identical edges top to bottom and left to right in Diagram 3 you have a torus. [✓]

(2.) String 1 in Diagram 4 can be derived as a 'double retrograde' followed by a (k,n)-perfect shuffle.

Let's say we are given a 'deck' (or set) of 12 pitch classes 0 through 11, and we divide it into k=3 cuts (subsets), each containing n=4 pcs:

[1,2,3,4], [5,6,7,8], [9,10,11,0].

A straightforward 3-way perfect shuffle of these three subsets would take the 'top' remaining element from each ordered subset consecutively and result in the permutation

[1,5,9,2,6,10,3,7,11,4,8,0].

Harmonically, this shuffle would result in four consecutive, equally-spaced augmented triads. But a 'perfect shuffle' doesn't depend on the internal order of each subset, only the order of choosing from each subset. So instead let's begin with a set of pcs cut into three stacks this way:

[9,10,11,0], [5,6,7,8], [4,3,2,1].

This reverses the order of the initial three tetrachords, and then reverses the order of internal elements in the last of the three retrograded chords. We then proceed to interleave this result left to right as a 3-way perfect shuffle. The result is string 1:

[9,5,4,10,6,3,11,7,2,0,8,1].

Note that reversing the final ordered sub-set to read [4,3,2,1] instead of [1,2,3,4], breaks the expected symmetry of equally spaced augmented triads, but the broken symmetry is replaced with a new trichord symmetry:

A : B :: B' : A'

where the As are SC-015 and the Bs are SC-037. A={4,5,9}, A'={8,0,1}=I5(A), B={3,6,10}, B'={7,11,2}=I5(B) (and, of course, the two hexachords are also related by I5). Checking back to Diagram 2 (l.h.) we see that in mm. 92–93 Messiaen grouped the 16th notes in 3's. His grouping appears to be intentionally drawing attention to the string's origin in a composite function drawing from these three sets since, by inspection, it can't possibly be functionally related to the right-hand line. [✓]
<<Added 11.10.15: String 1 is a variation of a pattern found in 'Mode de valeurs et d'intensités' identified as '7. Bars 86-96 (Group II)' (also '6. Bars 81-86 (Group I)' in retrograde) in Robert Sherlaw-Johnson (Messiaen, 1975, p.108, Table II)>>

(3.) String 2 results from successive spiral permutations. Start with the same initial chromatic clusters as we did in String 1, and label them A=[1,2,3,4], B=[5,6,7,8], C=[9,10,11,0]. The first spiral action (identical to a rotation) takes these tetrachords and rearranges them this way: A,B,C → B,C,A. The second spiraling takes the content of each tetrachord and rearranges it this way: [a,b,c,d] → [a,d,b,c]. So B,C,A= [5,6,7,8],[9,10,11,0],[1,2,3,4] becomes

[5,8,6,7],[9,0,10,11],[1,4,2,3],

which is string 2. The initial chromatic tetras are rearranged internally but kept intact harmonically (SC-0123) and related by T4. Checking back to Diagram 2 (l.h.) we see that in mm. 94–95 Messiaen grouped the 16th notes in 4's. Again, it looks like he was grouping by quadruplets according to this string's generating function operating on sets of four elements. [✓]
<<Added 11.10.15: String 2 is a variation of a pattern found in 'Mode de valeurs et d'intensités' identified as '4. Bars 53-57 (Group I)' in Robert Sherlaw-Johnson (Messiaen, 1975, p.108, Table II)>>

(4.) String 5 is generated by simple transposition, T5, from the seed string in passage C1 discussed in  Broken Symmetries 1.

[10,3,9,0,6,1,7,2,8,4,5,11] = T5([5,10,4,7,1,8,2,9,3,11,0,6]).

(... or was C1's seed string derived from String 5 by T7? At any rate ....)

String 5 functionally connects C2 to C1.

As shown in Diagram 2, in mm. 100-101, the 16ths are grouped in 3's, as they were generated in the entire C1 passage, mm. 70–75. [✓]

(It's as though Messiaen is leaving a trail for us by the way he groups sixteenths, relating that to the way the pitches were generated. But this idea is difficult to sustain beyond strings 1, 2, and 5.)

(5.) Strings 1 and 10 in Diagram 4 are related by a simple one-click rotation: the first element in string 1 (pc9) is moved to the end to generate string 10.

[9,5,4,10,6,3,11,7,2,0,8,1] → [5,4,10,6,3,11,7,2,0,8,1,9]. [✓]

(6.) (Hypothetical feature) So now we are left with strings 3, 4, 6, 7, 8, and 9 entirely unaccounted for. Is it possible there is a permutation that could relate all 10 strings, e.g., by interversion as in C1? Trivially, any pair of 12-strings could be treated as a permutation. But it would take a single covering permutation or group of related permutations to knit the matrix together such that we could claim a full solution to the question. For example, we can derive string 3 from string 2 by the permutation (5,4,9,3,11,0,6,7,2,10,8)(1), but this permutation doesn't relate any other pair of strings in the matrix. And the same for any other pair (just pick one element in any string and follow it through its position vis a vis all possible pairs – cf. Table 1 in Broken Symmetries 1). Also, none of these remaining strings can (thus far to me) be related by any permutation from an obvious/relevant external seed string as we found in strings 1, 2 and 5. The idea of knitting the whole matrix together by interversion (iterated permutation) or some obviously related group of permutations must be labeled [✕] as tentatively random. The reason the judgement remains tentative is due to the next feature observation. Examining the matrix columns, we find something else very suggestive that would seem to increase the odds against randomness for the matrix as a whole.

(7.) Column 5 reads down 6–9–3–5–6–9–3–5–6–3. Omitting the final element 3 which comes from the rotation of string 1 and might be redundant to the pattern, we get two identical vertical 4-string groupings with an extra element 6 tacked on the end: 6–9–3–5 / 6–9–3–5 / 6. Similarly, reading up we get the groupings 6–5–3–9 / 6–5–3–9 / 6.  Another way to look at this is by isolating the 6's: 6 / 9–3–5 / 6 / 9–3–5 / 6 down or 6 / 5–3–9 / 6 / 5–3–9 / 6 up. The middle 6 is element number 5 in string 5. This suggests that string 5, the string related by transposition from the seed string in section C1 is row-wise 'central' to the matrix and might  somehow generate the four strings above and below it. Another (better?) guess is that any string pair (n, n+4), where n=1,2,3,4, is related by some yet to be discovered function/transformation/generating principle. I have no idea how to calculate the odds against this symmetry appearing coincidentally in a random draw of ten 12-strings, but I would imagine it's huge. There's enough demonstrable consistency and planning evident to encourage me to continue searching for something I'm overlooking. So I mark this feature highly suggestive (that there is an undiscovered pattern) but inconclusive (and certainly not 'solved'). [?]

There are other features that suggest internal secondary patterns, but the ones above are the obvious ones. Pursuing them is quite a stretch, and the ones I know of are difficult to describe, far-fetched, often end in blind alleys, and (so far) wouldn't change or add anything to my present 'conclusion' about this passage. Obviously it is not possible at this point, given only the information above, to demonstrate that C2 was consciously organized as C1 clearly was – to wrap it up in a neat functional package where everything relates to everything else. Neither is it possible to declare that the unexplained portions are merely random.

.      .      .      .

My conclusion concerning the entire passage C2 is: no conclusion at all – at least in the sense of 'mission accomplished.' The evidence strongly suggests to me that all ten of the ghost strings in the  Magma Dance are derived and, less certainly, interrelated. I can't believe that Messiaen – especially Messiaen – would have functionally generated four 12-strings and then pulled in six random ones out of thin air. It is at least clear to me that in C2 he is conducting his earliest experiments in functional derivation/manipulation of material that go beyond the canonic T, R and I.

I invite others to take up the C2 challenge – and I will take it up again if I can think of an analytical attack I haven't tried – but as of now, I must follow in the steps of those befuddled jurists of old who wrote at the bottom of their undecidable cases:

NL

_____________________

* Pierre Boulez. 'Olivier Messiaen' ('Une classe et ses chimères', tribute to Messiaen on his fiftieth birthday from the programme for the Domaine musical concert of 15 April 1959. Tr. by Martin Cooper, 1986.) In Orientations: collected writings. Edition quoted: Faber & Faber, 1990. p.414.

[1] Ranges are given in scientific notation: C4 = middle C. Apologies for the confusion. I labeled the compositional scheme (Figure 1) without thinking I was planning on also talking about voice ranges. I'll use bold for the compositional scheme & italics for pitch notation here.

[2] Olivier Messiaen. 1994. Programme note in booklet accompanying Koch International Classics 3-7267-2 H1 quoted in Wikipedia article 'Quatre études de rythme'

[3] E.g., John M. Lee. 'Harmony in the Solo Works of Olivier Messiaen: The First Twenty Years.' In College Music Symposium. Vol. 23.

[4] In traditional notation, below is Diagram 4 with pitches as they appear in the score within the delimiting span F2–E3:

[5]

It was tempting at first to call this type of analysis 'inconsistency-tolerant' or even paraconsistent. Then, while reading the 1959 essay by Pierre Boulez from which the above quote is taken, I realized that the kind of analysis I was almost forced into by this section of Île de feu 2 was more precisely seen as a reflection of the 'conflict, or antinomy' Messiaen himself must have faced in creating this passage. In other words, the analytical process itself turns out to be antinomous.

Boulez identified such a feature of a work as a compositional conflict between spontaneity and organization. (One can easily believe he was speaking sympathetically here! The tug between the two has become endemic to music composition – as well as analysis – for more than a century.) So I have identified it similarly, viewing it from the other side, as an analytic-decision conflict between randomness and functionally created pattern. Fitting the present theme, it is also a study in persistent vs. broken symmetries which necessitates discriminating between invariant/covariant and unrelateable features.

[6] Four meditations on 'random.'

   (1) My use of 'random' in this context is not meant to imply its pejorative use accusing the composer of  'pick a note, any note, it doesn't matter', which, when reflected in analysis, is the oft used but seldom recognized academic's gloss, a wave of the hand signifying 'I have no idea, so let's move on.' I mean 'random' to be taken here in the sense of a placeholder for 'the analyst is stumped but [unlike the gloss] can't leave it alone.' This condition reminds one of the prince searching for Cinderella's foot which he assumes will eventually lead to Cinderella, not knowing in the light of day whether or not there is such a foot anywhere in the kingdom, or where the slipper came from, and increasingly facing the possibility that someone will finally dare tell him he spent the night dancing with a figment.

   (2) The word 'random' associated with the arts is often used loosely as a pejorative, but it has objective, non-pejorative meanings in the sciences. My usage here is meant to dismiss the former and respect, if not live up to, the latter. Any feature (say, in the descriptively generated matrix in Diagram 4) that can be shown to have been functionally derived from another feature (inside or outside the matrix) is a formally determined (non-random) feature, whether or not the composer is fully aware of such a determination in this formal sense. The probability that a formally determined feature of a 12-string (not to be confused with the guitar of the same name) could also have been arrived at by blindly drawing 12 notes out of a hat – tripped over, so to speak – is close to zero. Conversely, any feature that cannot be shown to be formally determined in this sense becomes a candidate for being judged analytically as a random feature, and such a feature remains forever a candidate. I add "candidate" as a hedge because it is close to impossible to be certain a feature is random in the sense I am using. How would one provide evidence for creative indeterminacy – call it inspiration or the angel, if you will? Even the composer can't be believed except in the case when s/he is divulging a determined feature (which Messiaen often did). The analyst simply has to learn to live in this suspension.

   (3) As I use the word 'random' in a music-analytic setting, any strictly aural ('it's just what I hear & I can't explain it') preference or other unalloyed preference (by the composer) for selecting one note or pitch-class row or interval string or chord or rhythm or other feature over another is a random selection that is potentially form-inducing. Again: my notion of randomness ignores the pejorative sense of 'pick any note, it doesn't matter'; but it preserves an essential place within techne for inspiration, serendipity, accident, and mistake.

   (4) This sets the stage for analysis of inconsistent features found embedded in a work. Such a feature potentially arises when a preponderance of evidence strongly suggests that a given feature surely must be determined, leading to the conclusion that either the formal determination (function, transformation, whatever) exists but cannot be found, or to the analyst's dreaded conclusion that the feature has no possible formal determination in a sense that relates to the context. It may persist in analytic limbo (undecidable) indefinitely, and its status as determined or random may never be decided definitively. Looked at one way a feature may be judged random, looked at another way it may be judged an un(re)solved determination.